Beim Digitalisieren gibt es eine Frage: mit welcher Auflösung müssen die Negative aufgenommen werden damit alle relevante Bildinformation erhalten bleibt? Dieser Frage gehe ich mal experimentell nach. Dazu nehme ich ein Bild und fotografiere es mit meiner Kamera bei unterschiedlichen Abbildungsmassstäben.
Methoden
Ausrüstung
Ich benutze eine etwas ältere Spiegelreflexkamera von Nikon, eine D300s. Sie hat einen Sensor im DX-Format (23.6 mm × 15.8 mm, Auflösung 4352 × 2868 Pixel), ist also etwa um den Faktor 1.5 kleiner als das Kleinbildformat (36 mm × 24 mm). Das Objektiv ist ein manuelles Micro Nikkor 55 mm 1:2.8 mit dem dazu vorgesehenen Zwischenring PK-13. Das ist eine excellente Optik, die kaum beobachtbare Verzeichnungen produziert, also ideal für diese Aufgabe.
Mit einem Abbildungsmassstab von 1:1.5 würde ich das Bild formatfüllend ablichten. Ich mag aber den schwarzen Rand, weshalb ich üblicherweise mit 1:1.7 arbeite. Dadurch verschenke ich etwas Auflösung.
Bild
Ich habe mir eine Gruppfenfoto aus dem Jahr 1989 ausgewählt, denn es enthält viele Personen und irgendwo wird sich sicher ein Detail finden, mit dem die Auflösung beurteilt werden kann. Jemand trug eine Halskette, die auf einer Seite in der Sonne, auf der anderen im Schatten war. Das finde ich ein gutes Detail. Ich habe das Bild mit mehreren Abbildungsmassstäben abgelichtet (den kann ich bei meinem Makroobjektiv ziemlich präzise einstellen). In Lightroom habe ich das Bild mit Negative Lab Pro invertiert.
Zum Bild noch ein paar Angaben, soweit sie rekonstruierbar sind. Der Film war ein Ilford FP4, den ich wohl bei ISO 125 belichtet hatte. Meist habe ich ID-11 als Entwickler benutzt, das wird wohl auch hier der Fall gewesen sein. Das ist ein feinkörniger Film der für so einen praktischen Test ziemlich geeignet ist. Die Kamera war eine Minolta Dynax 7000i. Das Objektiv war vermutlich ein 35-70 mm Zoomobjektiv. Das ist eine mittelmässige Linse von der keine Meisterleistungen zu erwarten sind.
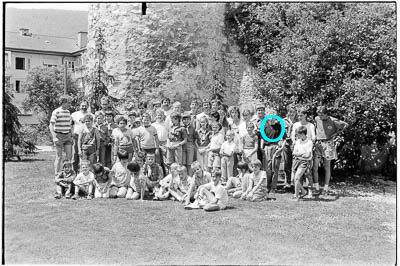
Ergebnis

Ich habe mir dann aus jedem Bild einen Ausschnitt in derselben Grösse ausgeschnitten (237 × 227 Pixel) und in Photoshop zu einem Streifen zusammengefügt (Fig. 1). Die Bilder habe ich mir dann auf dem Bildschirm vergrössert (wer das selber nachmachen will: das Bild lokal speichern und mit einem Bildbetrachtungsprogramm reinzoomen) und beurteilt.
Die Details sind bei allen Bildern zu erkennen, mit Ausnahme des Bildes im Abbildungsmassstab 1:2.0, wo z.B. die Kette im Schatten verschwindet. 1:1.7 scheint also vollauf ausreichend zu sein. 1:1.4 sieht vielleicht einen Tick besser aus, man darf sich aber nicht davon täuschen lassen, dass 1:1.4 grösser dargestellt wird. Fig. 2 zeigt eine Vergrösserung. Bei beiden sind die Details ausreichend gut zu erkennen, 1:1.7 ist also ein ausreichender Abbildungsmassstab.

Schlussfolgerungen
Mir scheint 1:1.7 keine schlechte Wahl zu sein, auch wenn 1:1.4 leicht mehr Details enthält. 1:1.0 ist sicher nicht notwendig. Das dort mehr sichtbare Korn mag zwar ästhetisch was bieten, aber wenn man das Bild komplett betrachtet, fällt kein Unterschied auf.
Der Test ist einfach gehalten und er hat mir einen nützlichen Wert geliefert. 1:1.7 ist praktisch, weil so auch bei kleinen Verschiebungen des Bildes auf dem Reprotisch immer noch alles erfasst wird.
Als kleinen Bonus kann die Auflösung eines Schwarzweissnegativs abgeschätzt werden. Bei 1:1.7 enthalten rund 88% der auf dem Sensor vorhandenen Pixel Bildinformationen. Der Rest ist Rand. Von den ca. 12.4 MP (Millionen Pixel) werden also etwa 11 MP genutzt. Das ist deutlich weniger als man auf Webseiten so als Angabe findet. Beispielsweise nennt [1] für einen Fujifilm Neopan Acros 100 mit einer Auflösung von 200 L/mm (Linien pro Milimeter) ein Pixeläquivalent von 35 MP (Kleinbild). Ilford FP4 hat fast sicher nicht diese Auflösung. Wenn ich das umrechne (Verhältnis 35 MP zu 11 MP und die Wurzel daraus [2]), erhalte ich bloss eher so 110 L/mm. Zudem umfasst mein Test reale und keine idealen Bedingungen, siehe meinen Kommentar zur benutzten Optik.
[1] https://www.photoscala.de/2010/06/26/wie-viele-megapixel-hat-ein-film/
[2] Die Wurzel braucht es, weil die Zahl der Megapixel ein Flächenmass ist und die Auflösung in Linien pro Millimeter ein Längenmass.